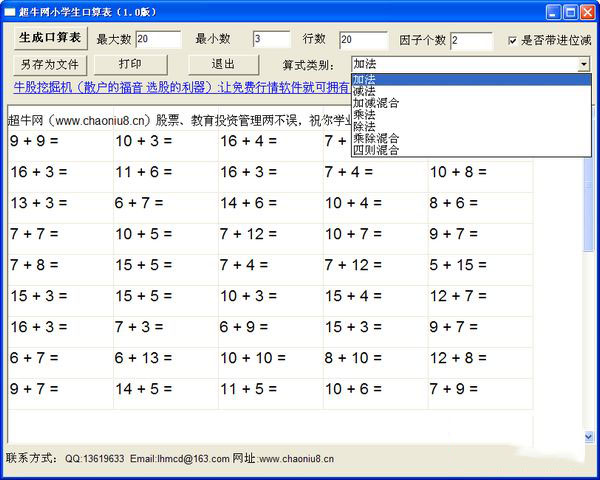
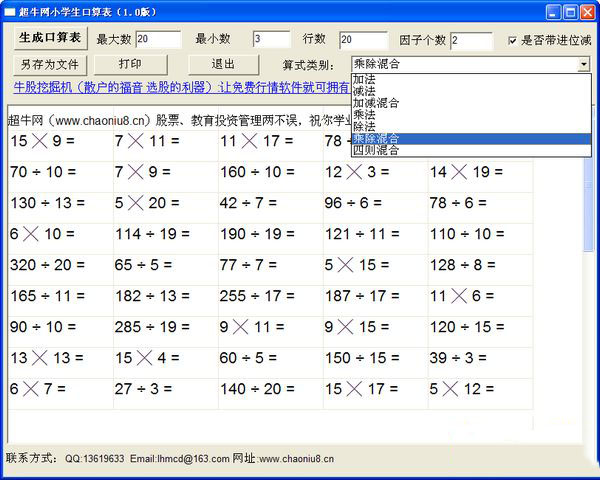
1、下载软件打开exe文件后，针对不同的孩子设置最大数，最小数，因子个数等。

2、设置完成后选择运算法，可以慢慢加大难度，最后点击生成口算表后，所有的口算题会在下面的框里显示，可以另存为文件。

3、如有需要则可以打印。

1、在没有括号的算式里，如果只有加减法或者只有乘除法，要从左往右依次计算，例如10.8-4.5+0.32=6.3+0.32=6.62

2、在没有括号的算式里，如果既有乘除法又有加减法，要先算乘除法，再算加减法，例如10.8-4.5×0.32=10.8-1.44=9.36

3、在有括号的算式里，要先算小括号里面的，再算中括号里面的，例如(10.8-4.5)×0.32=6.3×0.32=2.016

4、乘法速算 一、十位数是1的两位数相乘

5、个位是1的两位数相乘

6、十位相同个位不同的两位数相乘

7、首位相同，两尾数和等于10的两位数相乘

8、首位相同，尾数和不等于10的两位数相乘

9、被乘数首尾相同，乘数首尾和是10的两位数相乘

10、被乘数首尾和是10，乘数首尾相同的两位数相乘

11、两首位和是10，两尾数相同的两位数相乘

1、搬家性质

在同一级的运算中，其中的某一个数可以连同它前面的运算符号一起搬到另一个位置上，运算的结果不变

如：a-b+c=a+c-b;a÷b×c=a×c÷b

2、去括号的性质

在同一级的运算中，如果括号前面是加号或乘号，去掉括号时，括号里的运算符号不必变号：如果括号前面是减号或除号，那么在去掉括号时，括号里的符号就要变成与它相反的符号

如：a+(b-c)=a+b-c

3、减法的性质

一个数连续减去几个数，可以用这个数减去这几个数的和

如：a-b-c=a-(b+c)

4、除法的性质

一个数连续除以几个数，可以用这个数除以这几个数的积

如：a÷b÷c= a÷(b×c)

5、商不变的性质(b、c均不等于0)

a÷b= (a×c)÷ (b×c) a÷b= (a÷c)÷ (b÷c)

一、凑整法

就是运用加法和乘法的定律以及减法和除法的性质凑整计算，也就是凑成一个整千或整百、整十的数，直接进行简便运算

例1:3643-74+6357-126

=(3643+6357)-(74+126)

=1000-200

=800

通过观察题中数字的特点，引导学生运用加法的运算定律，将3643和6357相加凑成整千，利用减法的性质将74与126可凑成一个整百数，使计算简便

例2:125×25×4×8

=(125×8)×(25×4)

=1000×100

=100000

在这道连乘算式中，如果按常规从左往右依次计算，就比较麻烦，也不灵活，如果应用乘法的交换律和结合律，先算125与84的乘积，得到整千、整百的数，可使计算简便

例3:1400÷25÷4

=1400÷(25×4)

=1400÷100

=14

通过观察题中数字的特点，引导学生运用连除的运算规律，先将25和4相乘凑成整百，再用被除数除以这个整百使计算简便

二、去尾法

在减法计算时，若减数和被减数的尾数相同，先用被减数减去尾数相同的减数，能使计算简便

例1:2356-159-256

=2356-256-159

=2100-159

=1941

算式中第二个减数256与被减数2356的尾数相同，可以交换两个数的位置，让2356先减256，可使计算简便

三、提取公因数法

例1:39×28+75×28-14×28

=(39+75-14)×28

=100×28

=2800

引导学生观察数据特征，让学生发现三个乘法计算中有一个相同的因数28,另外三个因数39、75、14它们相加减后结果正好是100，就可以 逆用乘法分配律进行简算

四、分解法

1.分解成一个“积”

根据运算定律和数字特点，常常灵活地把算式中的数分解，重新组合，从而达到凑整简算

例1:25×32×125

= 25×(4×8)×125

=(25×4)×(8×125)

=100×1000

=100000

这道题将连乘算式中的因数32分解成4×8的形式，然后先将4与25和8与125相乘，得到整百数与整千数相乘的式题，比较简便

例2:8400÷140

=8400÷(7×20)

=8400÷7÷20

=1200÷20

=60

这道题中直接用8400除以140不能很快口算出得数，如果将140分解成7×20，那么先算8400÷7再除以20，就会很容易口算出结果

2.分解成一个“和”

就是把运算中的某一个数拆为一个整千或整百、整十数加一位数的和的形式，简化计算

例1:105×36

=(100+5)×36

=100×36+5×36

=3600+180

=3780

在这道题将接近整百数的因数105拆成100+5的和，再运用乘法分配律计算比较简便

3.分解成一个“差”

就是把运算中的某一个数转换成一个整千或整百、整十的数减一位数的形式，简化计算

例一:548+99

=548+100-1

=648-1

=647

这道题中将接近整百的加数99换写成100-1的形式，计算时先加整百数，再减一位数，比较容易

五、扩缩法

就是运用积不变规律及商不变性质，将算式中的数据扩大或缩小相同的倍数，从而使计算简便，做有些除法式题，可根据商不变性质进行简算。

例题1:

8500÷25

=(8500×4)÷(25×4)

=34000÷100

=340

在这道题中利用商不变规律，使被除数8500、除数25同时扩大4倍，得到整百数除多位数的算式很容易口算出结果

六、变形法

就是变换算式中的某个数据的表现形式，使其形变，从而运用运算定律简算

例题1:

25×37+75×21

=25×37+(25×3)×21

=25×37+25×(3×21)

=25×37+25×63

=25×(37+63)

=25×100

=2500

这道题从表面看似乎不能简便，但对题目的数字稍加对比、分析就可以看出，两个乘法算式中的因数25与75是有联系的，75正好是25的3倍,先将75×21改写成25×3×21，进而改写为25×63的形式，这样就产生了公因数25，就可采用乘法分配律进行简算